概念

应力

考虑一个有限且非常小的力 $\Delta F$ 作用在面积 $\Delta A$ 的区域内，当 $\Delta F$ 和 $\Delta A$ 趋于0时，其比值将趋于一个极限值，称之为应力。

正应力 (Pa)：

$$\sigma_z = \lim\limits_{\Delta A\rightarrow 0}{\frac{\Delta F_z}{\Delta A}}$$

切应力 (Pa)：

$$\tau_{zx} = \lim\limits_{\Delta A \rightarrow 0}{\frac{\Delta F_x}{\Delta A}}$$ $$\tau_{zy} = \lim\limits_{\Delta A \rightarrow 0}{\frac{\Delta F_y}{\Delta A}}$$

应变

单位长度线段的伸长或缩短称为正应变 (无量纲)：

$$\epsilon_{avg} = \frac{\Delta_s^{'} - \Delta_s}{\Delta_s}$$

初始相互正交的两条直线段间夹角的改变称为切应变：

$$\gamma_{nt} = \pi/2 - \lim\limits_{B\rightarrow A \text{ 沿 } n} \lim\limits_{C\rightarrow A \text{ 沿 } l}{\theta^{'}}$$

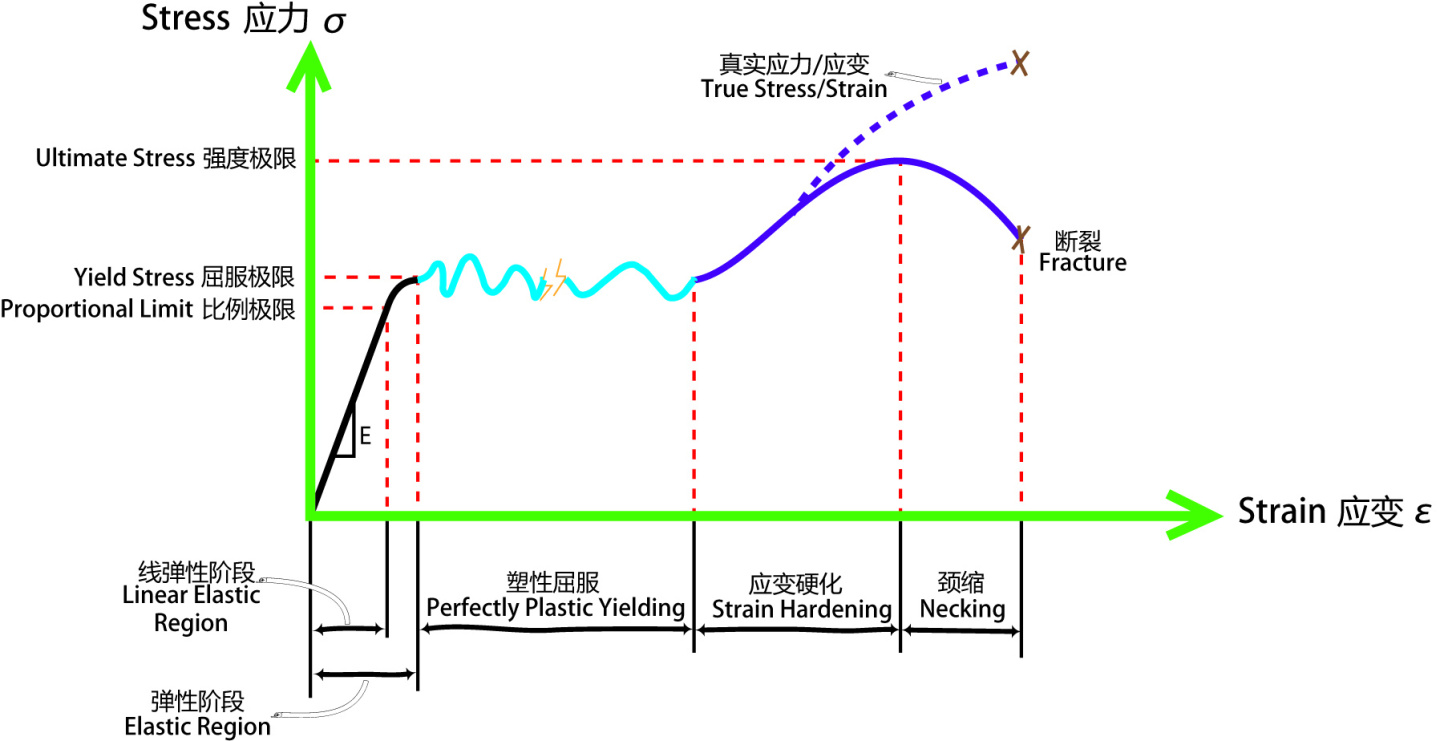
应力-应变曲线

弹性模量 E (Pa)

其中，E 称为弹性模量或杨氏模量。弹性模量是表征材料硬度的力学特征量。在弹性线性阶段，胡克定律（1676）为：

$$\sigma = E \cdot \epsilon$$

泊松比 $\nu$ (无量纲)

对圆杆施加载荷P，杆长度的生长量为 $\delta$，半径的缩短量为 $\delta_{'}$，对应的应变为：

$$\epsilon_{long} = \frac{\delta}{L} \quad \text{和} \quad \epsilon_{lat} = \frac{\delta_{'}}{r}$$

在线性弹性范围内，两应变之比为常数，称之为泊松比 $\nu$：

$$\nu = -\frac{\epsilon_{lat}}{\epsilon_{long}}$$

剪切胡克定律

$$\tau = G \cdot \gamma$$

三个材料常数的关系

$$G = \frac{E}{2(1+\nu)}$$